This page describes some standard methods employed for the analysis of complex chemical reaction mechanisms involving hundreds or thousands of reactions. Sections 1 to 4 contain routine techniques for the analysis of chemical mechanisms in complex reaction systems.
1. Law of Mass Action
The law of mass action is an empirical law that describes the rate of change of formation or consumption of species concentration in a chemical reaction. The rate law for a chemical reaction, which in the general case can be described by the reaction equation
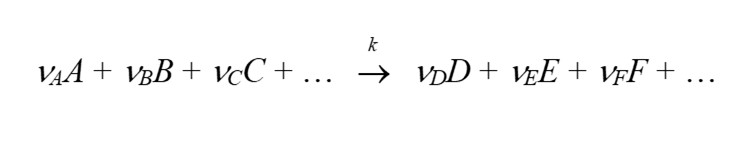
where A, B, C, … denote the different species involved in the reaction, and νA, νB, νC, … denote the stoichiometric coefficients for the reaction. Species A, B, C etc on the left hand side of the equation are called the reactants. Species D, E, F etc on the right hand side of the reaction are called the reaction products. Looking at the consumption of species A, B, and C, and the formation of species D and E, the reaction rate can be expressed according to
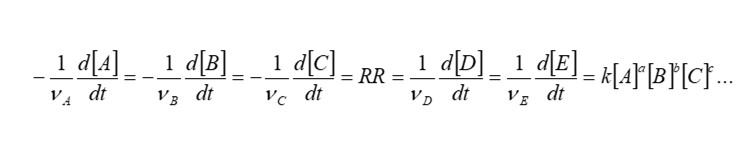
The values a, b, c appearing as exponential terms for [A], [B], [C] etc are named the order of the reaction. The overall order of the reaction is specified n = a + b + c + …. The value k that appears as a coefficient of the species concentrations on the right hand side of the above expression is known as the reaction rate coefficient. In chemistry, reactions are often studied at constant temperature, and k is then referred to as the rate constant. The reaction rate coefficient has a mathematical form which is linked to the Boltzmann factor for the probability of a reaction occurring, linked to the activation energy Ea required to initiate the reaction. It has an Arrhenius form, and is named the Arrhenius rate coefficient.

A simple chemical reaction of the form A -> B -> C + D through reaction rate coefficients k1 and k2, describes a reaction where reactant species A decomposes to form an intermediate species B at a rate defined by k1, which in turn, decomposes to form product species C and D at a rate defined by k2. The law of mass action predicts the solutions to the rate of reactions to be
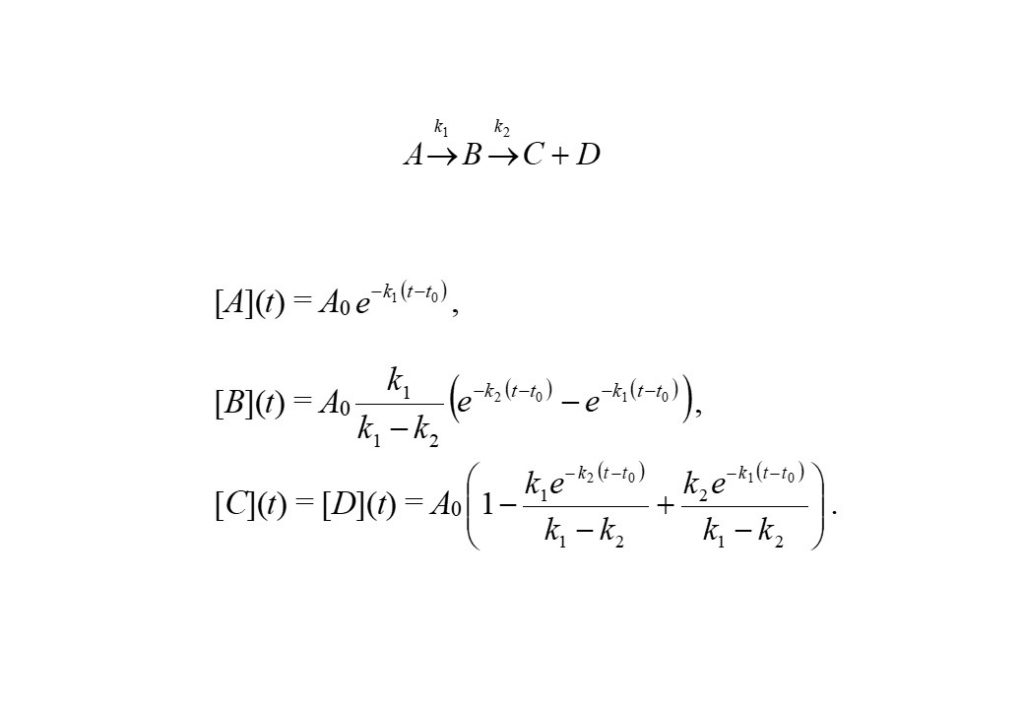
2. Quasi-steady-state or Quasi-equilibrium Approximation
Consider the above reaction again, A -> B -> C + D. B is an intermediate species, and if it decomposes as soon as it is formed (i.e. k2 >> k1), then it can be thought to be in a quasi-steady-state. The solutions can then be derived easily to be the following:
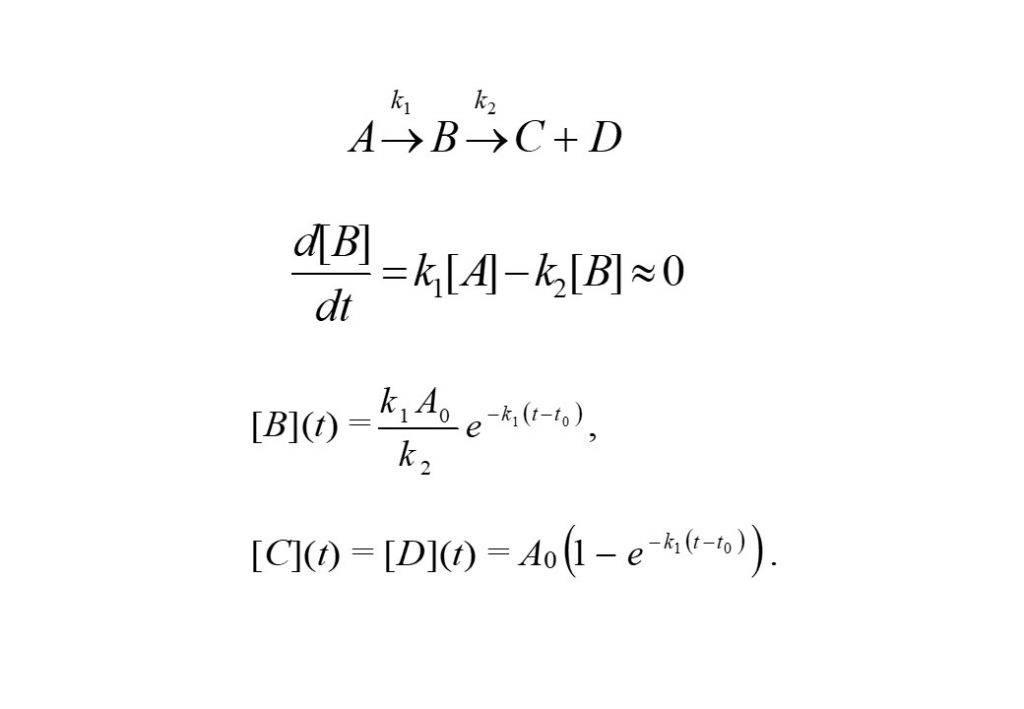
A more complex example is given below: the oxidation of molecular Hydrogen (H2) by molecular Bromine (Br2) to form Hydrogen Bromide (HBr). A proposed mechanism for the oxidation of Hydrogen by Bromine is given below. The reaction mechanism results in the formation of intermediate species Bromine atoms (Br), Hydrogen atoms (H), and the product species Hydrogen Bromide (HBr). M is called a bath gas molecule, and describes any one of the 6 species molecules present in the system colliding with Br2 to break it up to form 2 Br atoms (Reaction 1), or more unusually, colliding with 2 Br atoms to reform Br2 (Reaction 5). Reaction 5 is the reverse of Reaction 1.
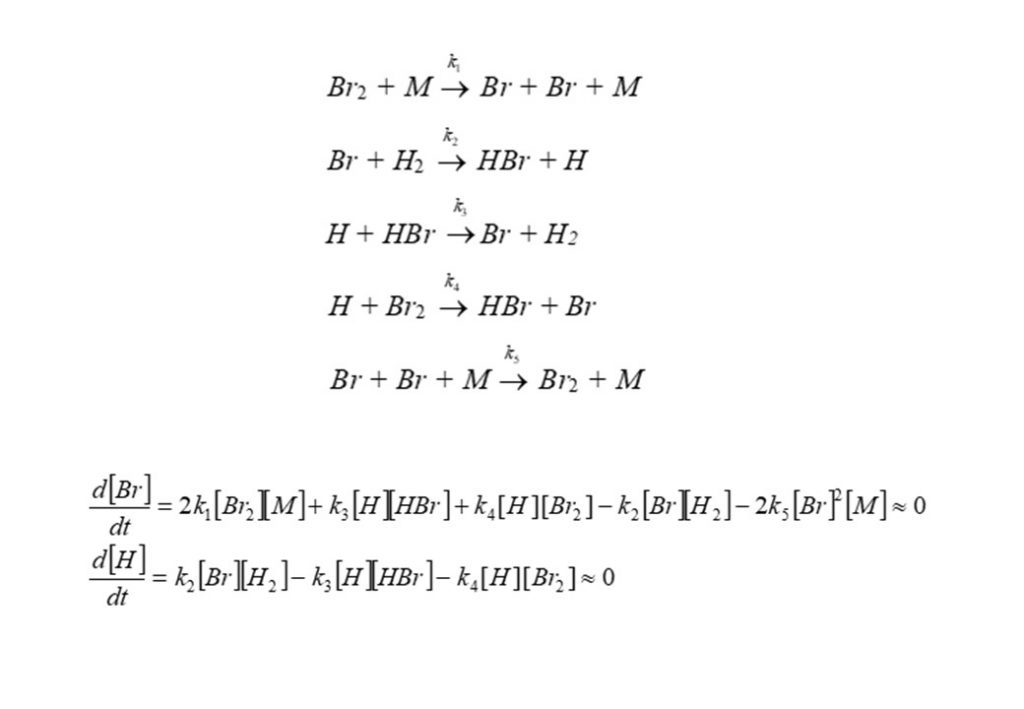
These equations can be solved to find the intermediate, quasi-steady state concentrations of atomic Bromine (Br) and atomic Hydrogen (H), and the rate of formation of Hydrogen Bromide (HBr).
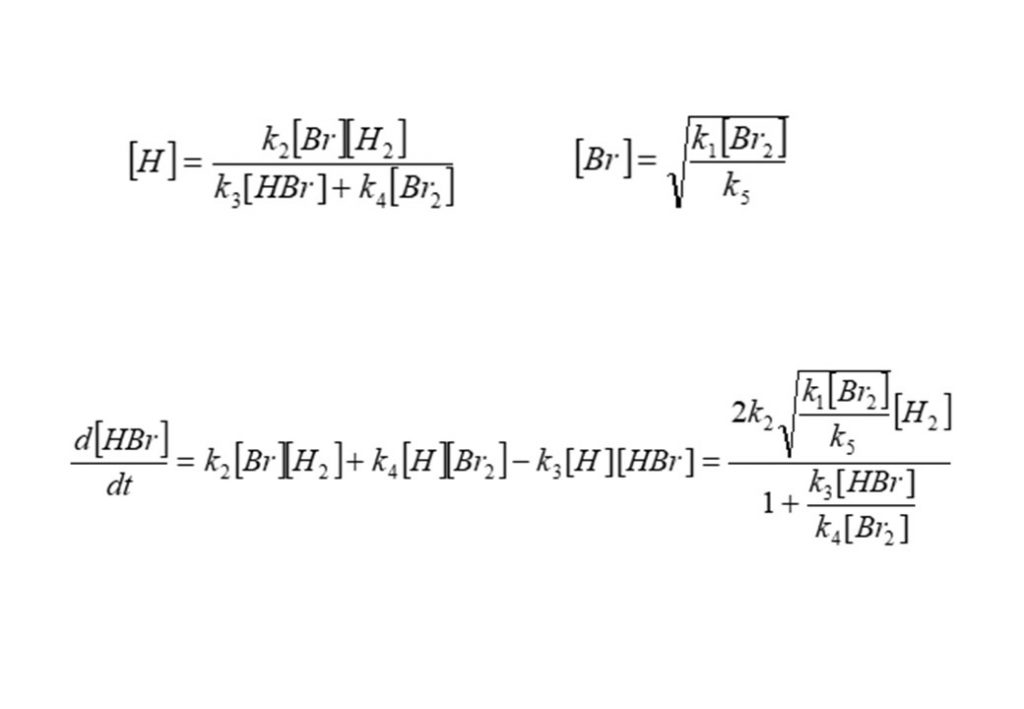
Another interesting example of the quasi-equilibrium approximation is in the high temperature oxidation of molecular hydrogen (H2) by molecular Oxygen (O2), to form water (H2O). The proposed mechanism for the oxidation process is the following, shown on the top left of the frame below. Assuming these reactions are in equilibrium enables the equilibrium equation (top right). This enables quasi-equilibrium solutions to be found for the concentrations of Hydrogen atoms (H), Oxygen atoms (O), and Hydroxyl radical molecules (OH).
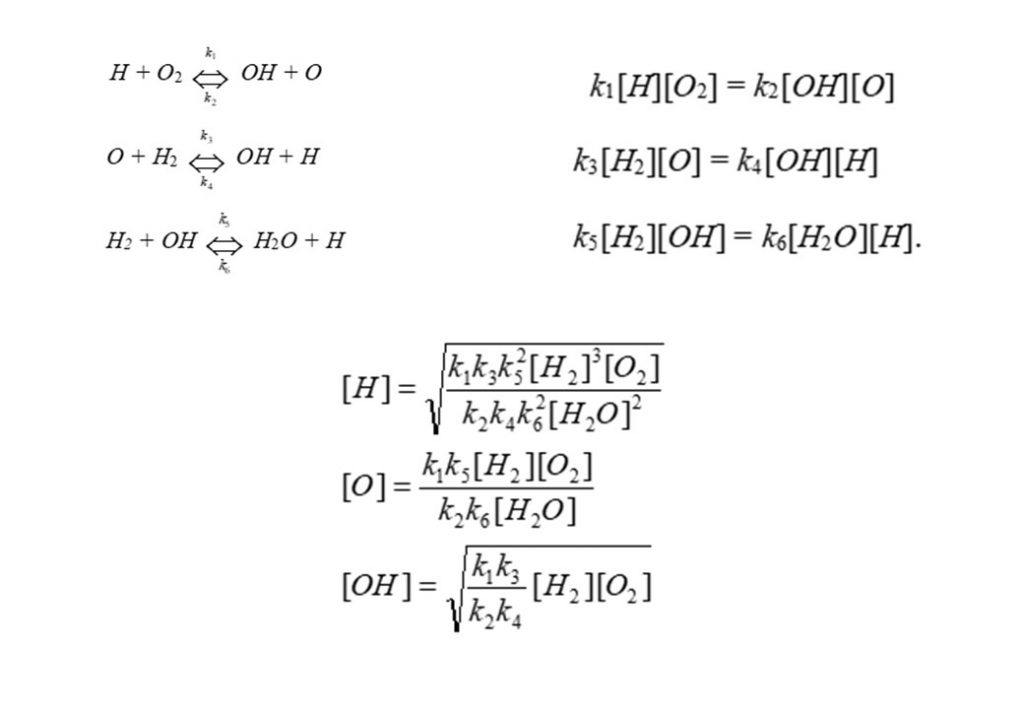
Prior to the development of computers, this was a powerful technique used to simplify chemical kinetic analysis of reaction mechanisms involving unstable, reactive intermediate species. Note from the above that it enables the simplification of a differential equation to an algebraic equation.
3. Reaction Path Analysis
Finding the trajectory solution to a reaction system that evolves with chemical species reacting to form new species as a function of internal or external thermodynamic properties like pressure, temperature and volume, first requires a mathematical formulation. This is conventionally done by expressing the chemical species concentrations in vector form (y(t)), where the elements of the vector y are just the species concentrations [Y]i. We can then write a first order differential equation for the rate of change of the species concentrations in the form dy/dt. The equation for dy(t)/dt can then be expressed in the form dy(t)/dt = A(T).y + B(p,T):yy + C(p,T)yyy = f(y). This equation contains three terms: the first term originating from the mechanism containing molecules that undergo thermal decomposition, the second term originates from bi-molecular collision processes, and the third term originates from molecules that undergo termolecular collision processes (3-body collisions). This equation for dy(t)/dt can be numerically integrated subject to the initial conditions and changing thermodynamic properties. The Figure below contains the results of a numerical integration of the chemical kinetic solution trajectory for a methanol-air auto-ignition process.
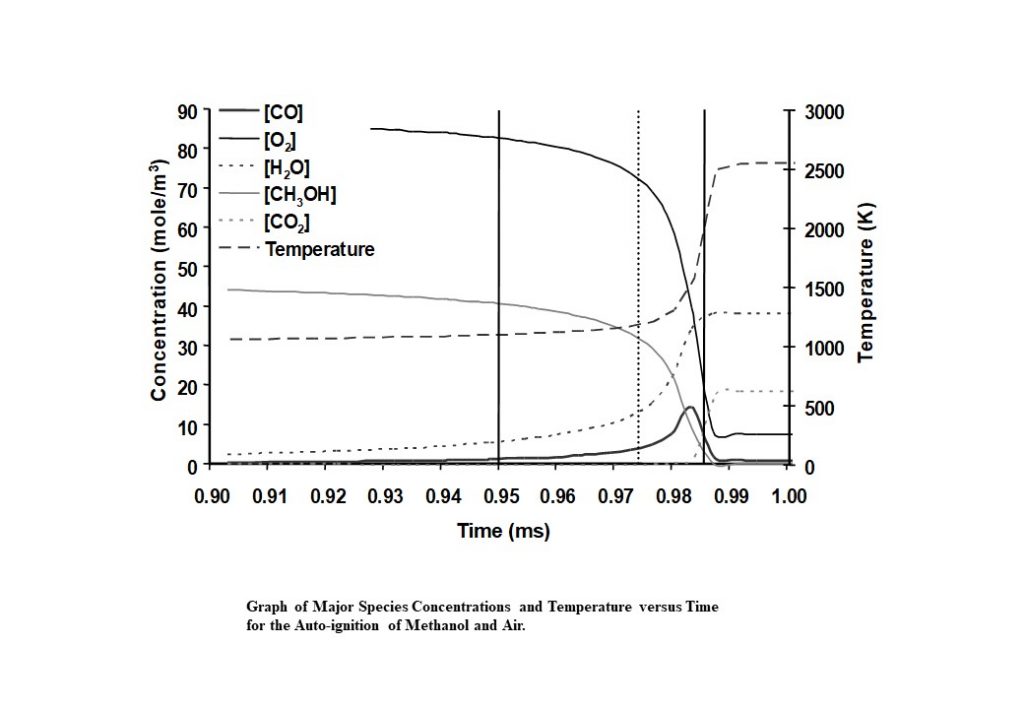
The numerical integration is a time-step integration, with the integration algorithm capable of adjusting time steps, depending on the complexity of the local chemistry. Such systems are said to be “stiff”, in that there are as many timescales as there are species comprising the system, and these timescales can vary by many orders of magnitude. The numerical integrator used to integrate such systems must be capable of coping with the numerical errors that can arise from the very different time-scales present in the system. Most of these use a variation of Gear’s method in the algorithm. The fuel specified in this example is a simple fuel, and its combustion is described by the behaviour of 20 species (CH3OH, CH3O, CH2OH, CH2O, CHO, CO, CO2, H2O, H2, O2, N2, H, O, OH, HO2, H2O2, CH4, CH3, CH2, CH) involved in the auto-ignition process.
At each time-step, the integration algorithm determines the rates each reaction contributes to the formation and/or consumption of species. This can then be employed to discover which reactions are contributing to the formation/consumption of individual species involved in the auto-ignition. This is the basis of a reaction path analysis.

Table 1 is a matrix of numbers with rows identifying the reaction number in the mechanism, and the columns identify each of the species involved in the reaction. Each reaction will contribute a reaction rate for a particular subset of species at a given time step in the evolution of the system. An alternative representation of the reaction path is provided in the Figure below, which describes the reaction routes at a given point in time.
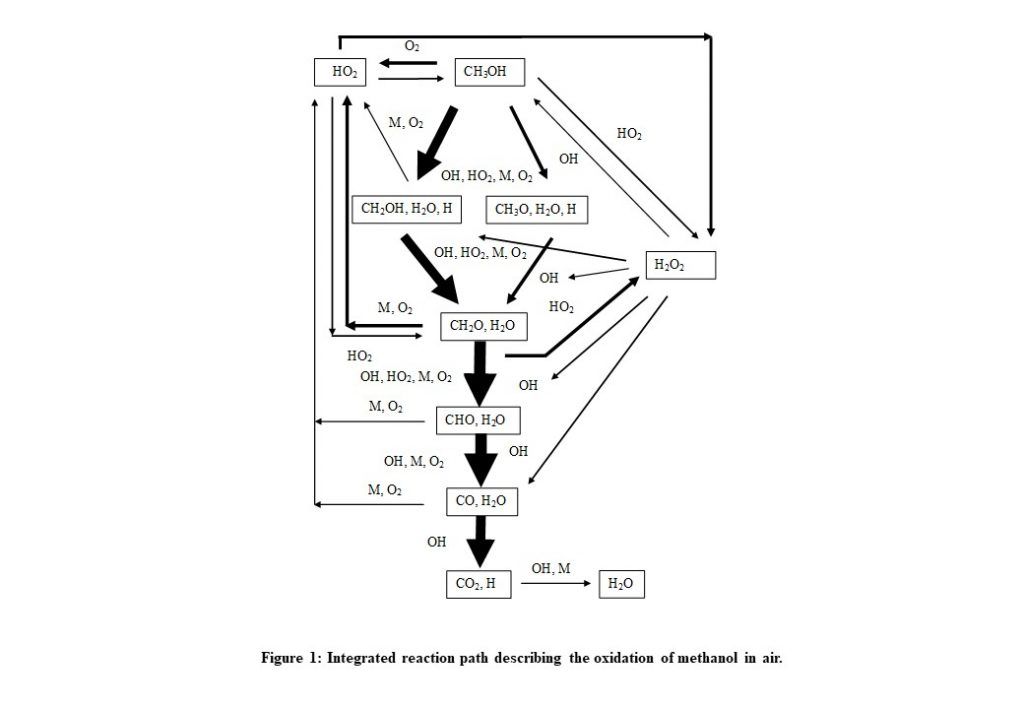
The thickness of the arrows indicate the strength of the reaction in contributing to the formation/consumption of a particular species involved in the combustion process.
4. Sensitivity Analysis
Sensitivity analysis is employed to discover the sensitivity of the temperature or concentration of a species formed or consumed in a complex reaction mechanism to a variation in the reaction rate coefficient for a particular reaction in the mechanism. In order to be comparable with other sensitivities, the sensitivity is a normalized quantity. In order to illustrate this, consider the example of the simple reaction system specified at the top of this page.
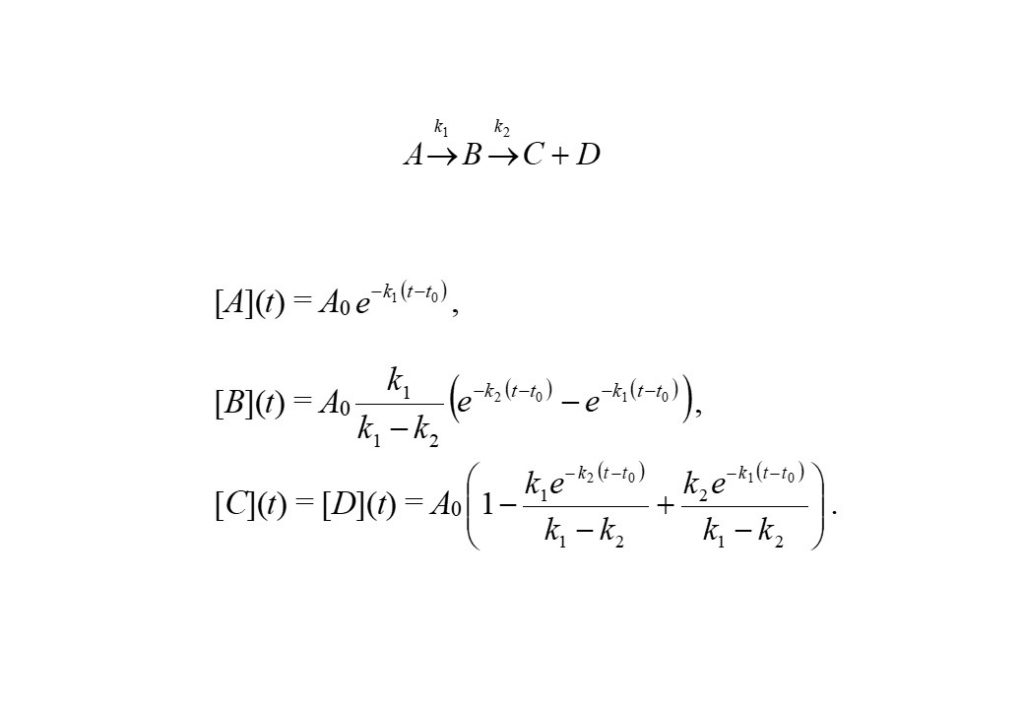
The sensitivities of the concentrations of product species C and D to reaction rates k1 and k2 are defined to be:
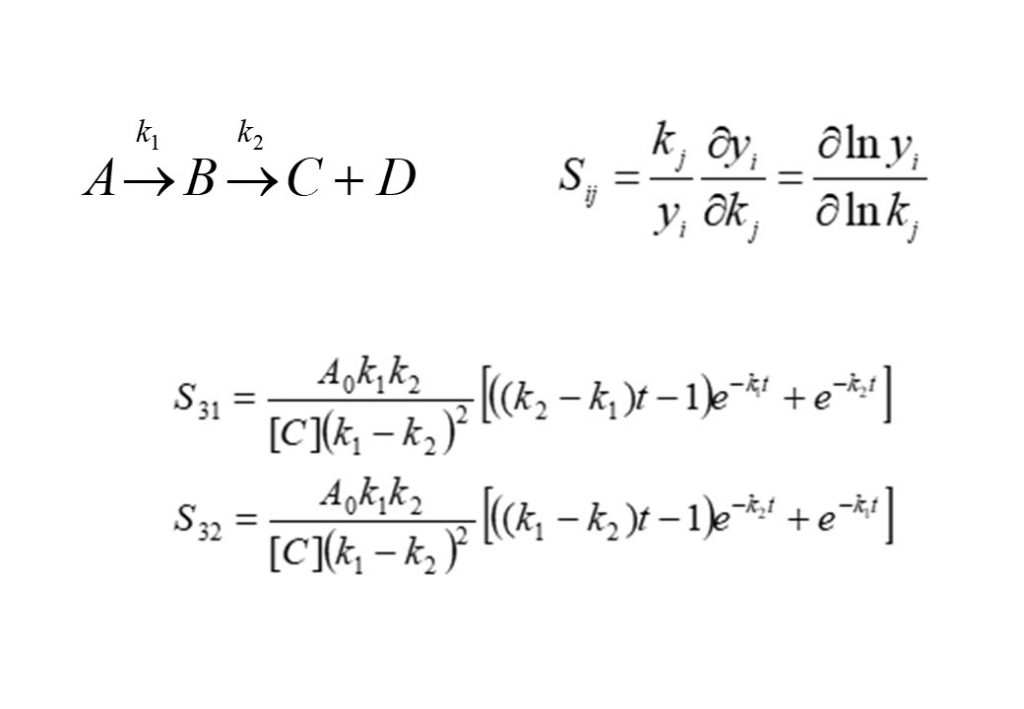
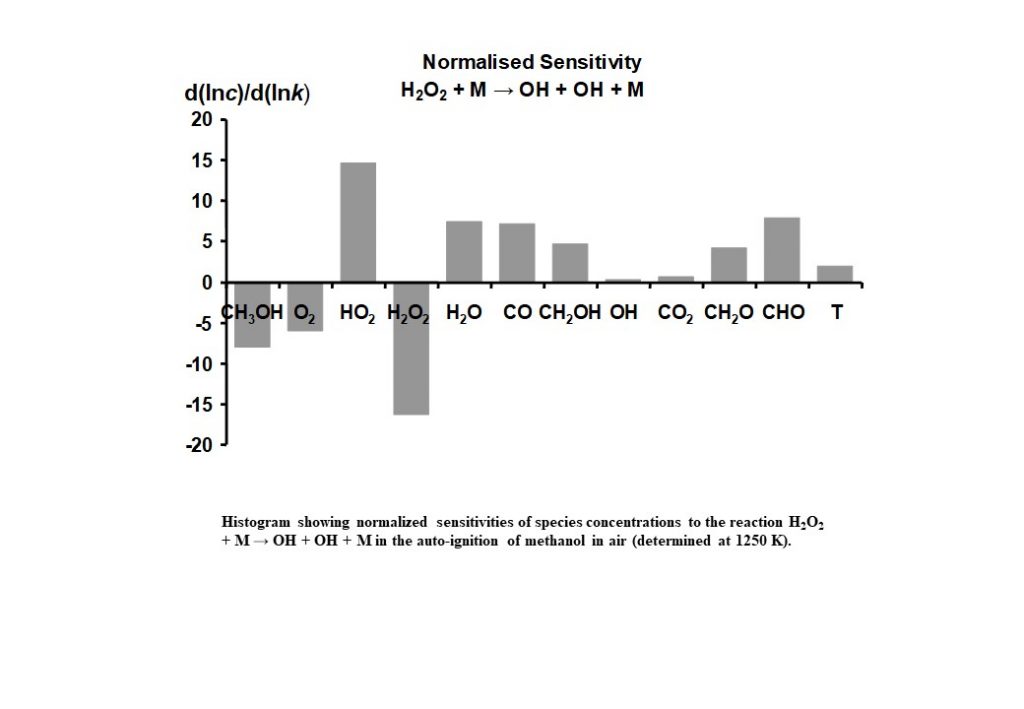
Going back to our earlier example of methanol-air auto-ignition, the Figure below shows the relative sensitivity of the most important species involved in the system to a variation in the reaction rate coefficient k for one of the key reactions in the methanol-air auto-ignition system (the collision induced thermal decomposition of hydrogen peroxide to hydroxyl radicals).